Você entende a importância do método de ensemble ao entrar no universo do Machine Learning e ficar perdido com a quantidade de estimadores que temos a disposição.
Temos regressão linear, polinomial e logística, gradiente descendente, XGBoost, máquina de vetores de suporte, naive bayes, árvores de decisão, Random Forest, entre outros.
Todos esses estimadores diferem uns dos outros, pois cada um parte de uma hipótese para tentar entender melhor como os dados se comportam, e assim poder realizar previsões mais robustas.
Vamos falar neste artigo sobre como reunir os pontos fortes de cada modelo individual.
Diferenças entre os estimadores
Antes de entender as vantagens do método de ensemble, você precisa entender as características individuais de alguns estimadores.
Gradiente Descendente
Por exemplo, o estimador de gradiente descendente propõe um valor aleatório inicial para o grupo de parâmetros e calcula o valor da função de custo, que basicamente mede o quanto as previsões do modelo estão distantes dos valores reais.
Esse processo pode ser visualizado na figura abaixo, onde θ* representa o grupo de parâmetros que minimizam o custo, ou seja, que fazem com que as previsões do modelo sejam mais próximas dos valores reais.
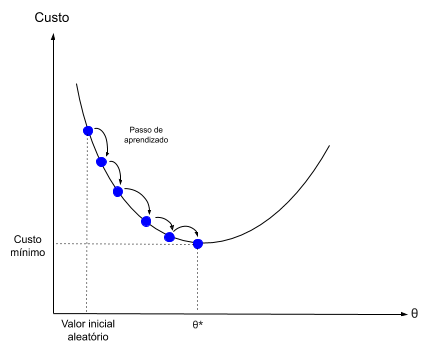
Após esse cálculo inicial, há uma variação no valor dos parâmetros e novamente é calculado o valor da função de custo. Esse ajuste dos parâmetros é feito diversas vezes, até que os parâmetros que minimizam a função custo sejam encontrados.
Máquina de Vetores de Suporte (SVM)
Por sua vez, na construção de um modelo de classificação, a máquina de vetores de suporte procura estabelecer uma linha de separação entre os dados relativos às diferentes classes.
Essa relação é mais fácil de ser entendida visualmente, conforme a figura abaixo.
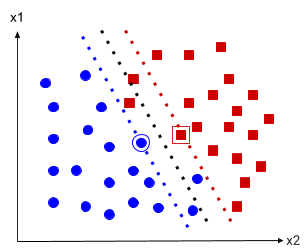
A linha pontilhada preta representa a fronteira de decisão do modelo de vetores de suporte, tudo que está à esquerda da linha pontilhada preta o modelo classifica como uma bolinha azul, ao passo que tudo que está a direita é classificado como um quadrado vermelho.
A linha azul pontilhada e a vermelhada pontilhada são chamadas de vias, e a bolinha azul e o quadrado vermelho em destaque, são os vetores de suporte, razão do nome do estimador.
Os vetores que estão entre as linhas azul e vermelha estão violando a margem, no caso, o modelo procura achar a maior distância possível entre as duas linhas coloridas, mas com o menor número de violações.
Árvore de Decisão
De forma muito mais intuiva e passível de ser feita até manualmente, temos o algoritmo de árvore de decisão.
Basicamente, o algoritmo determina um ponto de divisão em uma determinada categoria, de forma a separar melhor as diferentes classes.
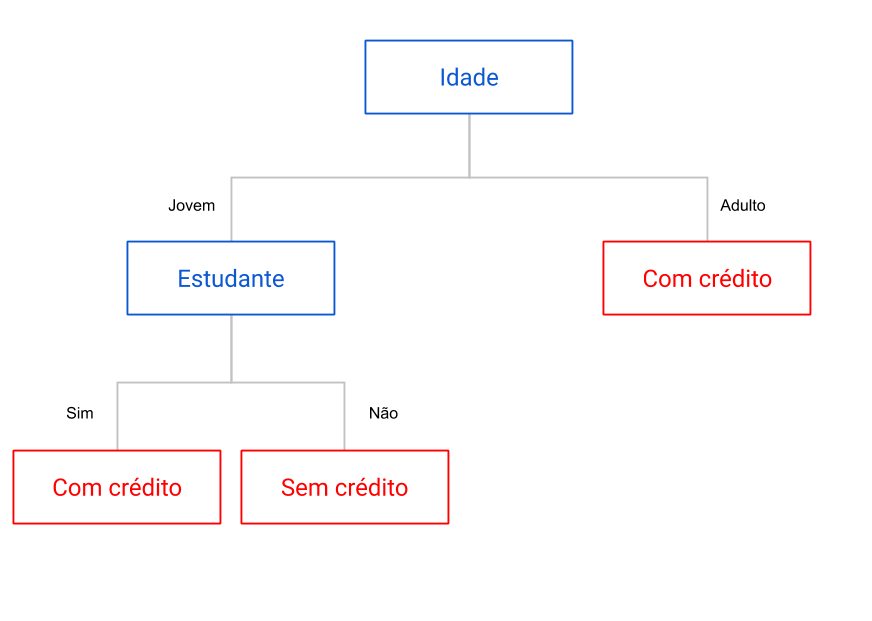
Por exemplo, digamos que você trabalha em um banco e quer saber se deve ou não disponibilizar um valor maior de crédito para um determinado cliente, e para isso monta uma árvore de decisão. Essa árvore pode ser visualizada na figura acima.
A primeira etapa da árvore determina se o cliente é adulto ou jovem. Se for adulto, você pode disponibilizar o crédito, caso contrário você deve olhar se o cliente é ou não um estudante. Sendo estudante, você pode disponibilizar um crédito extra, caso contrário, o crédito não deve ser disponibilizado.
O algoritmo de árvore de decisão faz exatamente isso, mas claro, de forma muito mais completa, analisando várias categorias e diferentes pontos de divisão.
Comparando os 3 modelos
Dada essa breve explicação sobre três estimadores, podemos perceber que as hipóteses utilizadas em cada um pra observar o relacionamento entre os dados, são bem diferentes entre si. Com essa diferença, é crível pensar que as previsões feitas por cada estimador podem também ser diferentes.
Para observar essas diferenças nas previsões, estimei três modelos utilizando gradiente descendente (SGDClassifier), máquina de vetores de suporte (SVC) e árvore de decisão (DecisionTreeClassifier), com o objetivo de prever se um determinado passageiro do Titanic sobreviveu ou não ao acidente.

Esse é um desafio muito famoso do Kaggle, se você não conhece sugiro ler os dois artigos aqui do Sigmoidal que falam sobre esse desafio.
Os modelos estimados utilizaram somente os dados de treino disponibilizados pelo Kaggle, pois era necessário saber se um passageiro sobreviveu ou não ao acidente pra observar a diferença nas previsões.
Como os estimadores de gradiente descendente e vetores de suporte são sensíveis a escala dos dados, fiz o escalonamento utilizando o StandardScaler. O código completo do projeto pode ser visto aqui.
Realizando as previsões dos três modelos, observe os seguintes resultados para cinco passageiros em específico.
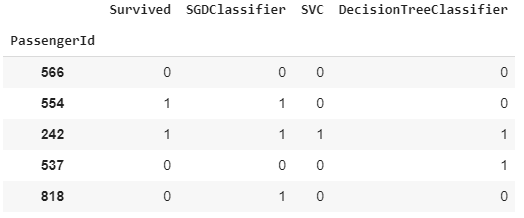
A coluna Survived nos diz se o passageiro realmente sobreviveu, valor 1, ou não, valor 0.
Temos que para o primeiro passageiro, 566, os três modelos previram corretamente que ele não sobreviveu, ao passo que para o terceiro passageiro, 242, os três modelos previram corretamente que ele sobreviveu.
Para o segundo passageiro, 554, somente o modelo de gradiente descendente fez a previsão correta, mas esse estimador foi o único que errou a previsão do último passageiro, 818.
Para o quarto passageiro, 537, os modelos de gradiente descendente e vetores de suporte foram assertivos na sua previsão, mas o modelo de árvore de decisão cometeu um erro.
A questão é que não há um modelo perfeito, se não seria fácil demais criar modelos de Machine Learning.
O ponto aqui é ressaltar que para alguns passageiros, certos modelos performam de maneira mais satisfatória em relação a outros.
Existe uma maneira simples de criar um estimador capaz de reunir os pontos fortes de cada modelo individual, é o chamado Classificador de Votação.
Método de Ensemble – Classificador de Votação
Esse classificador é um método de ensemble, que basicamente tem como objetivo combinar as previsões de diversos modelos, sendo que a previsão final é aquela que ocorre com maior frequência.
Por exemplo, observe abaixo o resultado do classificador de votação para os mesmos cinco passageiros analisados anteriormente. No caso, o VotingClassifier fez a combinação dos três modelos.
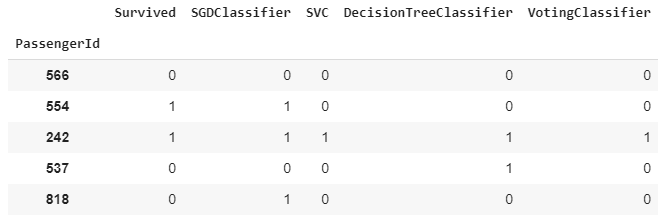
Para o primeiro passageiro, não houve resultado distinto, todos os modelos tiveram como resultado que o passageiro não sobreviveu, logo, o classificador de votação manteve esse resultado.
O mesmo é observado no resultado para o terceiro passageiro. Para o quarto passageiro, dois modelos previram que o passageiro não sobreviveu, enquanto um modelo previu que ele tinha sobrevivido.
Nesse caso, o classificador de votação determina como previsão final que o passageiro não sobreviveu, dado que mais estimadores alegaram esse resultado. Podemos observar essa relação assertiva de decisão pela maioria, também no resultado do último passageiro.
Claro que esse classificador não é perfeito.
Para o segundo passageiro, o modelo de gradiente descendente foi o único que previu corretamente o resultado. Como a maioria dos estimadores errou, o classificador de votação também errou.
Essa relação de maioria é chamado de hard voting, mas há também o soft voting, no qual o resultado final é baseado na probabilidade do valor ser 0 ou 1.
Mas para isso, o estimador usado deve dar suporte a previsão baseada em probabilidades de ocorrência das classes, coisa que o gradiente descendente e a máquina de vetores de suporte não fazem diretamente.
Para saber mais sobre essa diferenciação, sugiro dar uma olhada na documentação do classificador de votação.
Desempenho do Método de Ensemble
Mesmo cometendo erros, como observado para o segundo passageiro, o classificador geralmente consegue performar melhor do que os estimadores individualmente. De acordo com Aurélien Géron [1],
mesmo que cada estimador seja um aprendiz fraco (o que significa que sua classificação é apenas um pouco melhor do que adivinhações aleatórias), o conjunto ainda pode ser um forte aprendiz (alcançando alta acurácia).
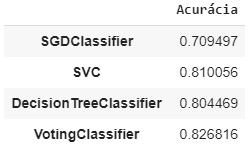
Podemos observar essa característica ao obter a acurácia de cada modelo individualmente, além da acurácia com o classificador de votação. Esse resultado por ser visualizado abaixo.
No caso, o modelo de máquina de vetores de suporte é o que performa melhor entre os modelos individuais, mas ainda assim é uma performance pouco pior que do classificador de votação.
Porém, ao utilizar o VotingClassifier devemos nos preocupar com um detalhe: os estimadores utilizados em conjunto devem ser bem diferentes.
Isso é necessário porque a hipótese do classificador de votação é que os estimadores devem ser independentes, ou seja, os erros dos modelos devem ser não correlacionados.
Como os modelos são treinados com os mesmos dados, o que já aumenta a chance de correlação dos erros, devemos utilizar pelo menos estimadores com hipóteses diferentes, como as que foram descritas no início do artigo.
A razão disso é óbvia, dado que os dados de treino são os mesmos, se os estimadores forem parecidos, cometerão os mesmos erros, o que torna inútil o uso do classificador.
Tendo atenção a esse detalhe, o uso do classificador é bastante útil para melhorar a acurácia dos modelos de classificação, como já visto anteriormente.
Para ratificar esse detalhe, eu estimei os mesmos três modelos individualmente e combinando também com o VotingClassifier utilizando todos os dados de treino disponibilizados pelo Kaggle,e testei nos dados de teste com o objetivo de submeter as previsões no desafio do Titanic (lembrando que os códigos podem ser vistos aqui). Nas figuras abaixo podemos observar os resultados obtidos.




No caso, o classificador de votação também performou melhor do que os estimadores individuais nos dados de teste, obtendo um score mais elevado.
Combinando essa técnica de ensemble com métodos de otimização e feature engineering, podemos melhorar ainda mais nossos resultados. Mas isso fica para um próximo artigo!
Para qualquer dúvida, opinião, sugestão, deixe um comentário aqui no post ou entre em contato comigo lá no LinkedIn! Vou gostar de ter seu feedback.
Referência:
[1] Hands-On Machine Learning With Scikit-Learn and TensorFlow. Aurélien Géron, 2017.




















