O Problema da Mochila, também conhecido como “Knapsack Problem”, é um desafio clássico na teoria da otimização combinatória. Ele tem aplicações em uma variedade de campos, oferecendo uma abordagem eficaz para resolver problemas de alocação de recursos limitados.
O que é o Problema da Mochila?
Imagine que você está preparando uma mochila para uma trilha, e precisa levar a melhor combinação de itens possível. Cada item tem um peso e um valor associado.
O objetivo é selecionar os itens de forma a maximizar o valor total, respeitando a capacidade máxima da mochila.
Existem duas versões principais do problema:
-
Problema da Mochila 0/1
– Cada item pode ser incluído (1) ou excluído (0), sem possibilidade de frações. Nesse caso, a quantidade de possibilidades é reduzida, e o problemas é um pouco mais simples, pois não podemos dividir os itens.
-
Problema da Mochila Fracionária
– Frações de itens podem ser incluídas, permitindo uma abordagem mais flexível. Dessa forma, há mais possibilidades, e mais pontos a serem observados.
Relevância e Aplicações
O Problema da Mochila é relevante em várias áreas devido à sua capacidade de modelar situações do mundo real que envolvem decisões de alocação de recursos. Algumas das áreas de aplicação incluem:
-
Logística e Supply Chain
– Otimização de carga em caminhões e contêineres para maximizar o valor dos itens transportados. Também podemos levar em consideração questões de rotas, abastecimento, e muito mais.
-
Finanças
– Alocação de recursos em carteiras de investimento, considerando limitações de capital.
-
Biologia
– Seleção de genes para maximizar a aptidão em algoritmos genéticos.
-
Computação Gráfica
– Otimização de texturas e elementos gráficos em jogos ou simulações.
-
Publicidade Online
– Seleção de anúncios para maximizar o retorno sobre o investimento considerando limitações de espaço. Aqui também podemos falar sobre Marketing Mix Modeling, otimizando investimento em diferentes canais de mídia.
Possíveis Soluções para o Problema da Mochila
-
Métodos Brutos
– Soluções de força bruta, como a verificação de todas as combinações possíveis, são viáveis para conjuntos de dados pequenos. No entanto, sua eficácia diminui rapidamente com conjuntos maiores de dados devido à explosão combinatória.
-
Programação Dinâmica
– A abordagem de programação dinâmica é eficaz para o Problema da Mochila 0/1. Ela divide o problema em subproblemas menores, resolvendo-os e combinando as soluções para obter a solução global.
– A tabela de programação dinâmica é preenchida gradualmente, começando pelos subproblemas menores até alcançar a solução completa.
-
Algoritmo Guloso (Greedy)
– O algoritmo guloso escolhe o item de maior valor ou benefício por unidade de peso em cada iteração. Embora seja computacionalmente eficiente, não garante sempre a solução ótima, especialmente no Problema da Mochila 0/1.
-
Algoritmos Metaheurísticos
– Algoritmos como algoritmos genéticos, algoritmos de colônia de formigas e simulated annealing são eficazes para encontrar soluções aproximadas em problemas complexos.
Exemplo Prático
Considere uma mochila com capacidade de 10 unidades e os seguintes itens:

Utilizando programação dinâmica, podemos construir a seguinte tabela:
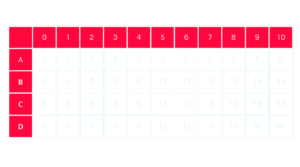
A célula na última linha e última coluna (20) indica o valor máximo que podemos obter com a capacidade da mochila especificada.
O Problema da Mochila é um desafio fascinante e versátil que oferece insights valiosos em situações práticas de alocação de recursos.
Compreender suas aplicações, desafios e diversas abordagens de solução permite a otimização de decisões em uma variedade de setores.
Ao desvendar as complexidades do Problema da Mochila, podemos aproveitar seu potencial para aprimorar estratégias e maximizar o valor em situações do mundo real.
Avance com curiosidade, experimente e descubra as possibilidades que o Problema da Mochila oferece no domínio da otimização e tomada de decisões.




















