O Que é Amostragem e Quantização no Processamento de Imagens

Você já parou para pensar no que acontece entre o momento em que a luz entra pela lente de uma câmera, é projetada no ponto focal, atravessa o filtro de Bayer, atinge o sensor… e então aquela onda eletromagnética se transforma em um array de números que representa a imagem capturada?

Como uma onda contínua do mundo real pode ser transformar em uma matriz com valores entre 0 e 255?

Neste artigo, eu vou te mostrar o princípio básico por trás da formação de imagens digitais. Vamos entender como uma imagem digital pode ser formada através de dois processos fundamentais: amostragem e quantização.

O código-fonte completo com os exemplos em Python está disponível logo abaixo. E se você quiser se aprofundar mais em Visão Computacional, clique aqui para conhecer a Pós-Graduação da Sigmoidal.

Amostragem e Quantização

Assim como para Aristóteles o movimento é a passagem da potência ao ato, a criação de uma imagem digital representa a atualização de um potencial visual contínuo (capturado pela luz) em um conjunto finito de dados discretos, por meio da amostragem e da quantização.

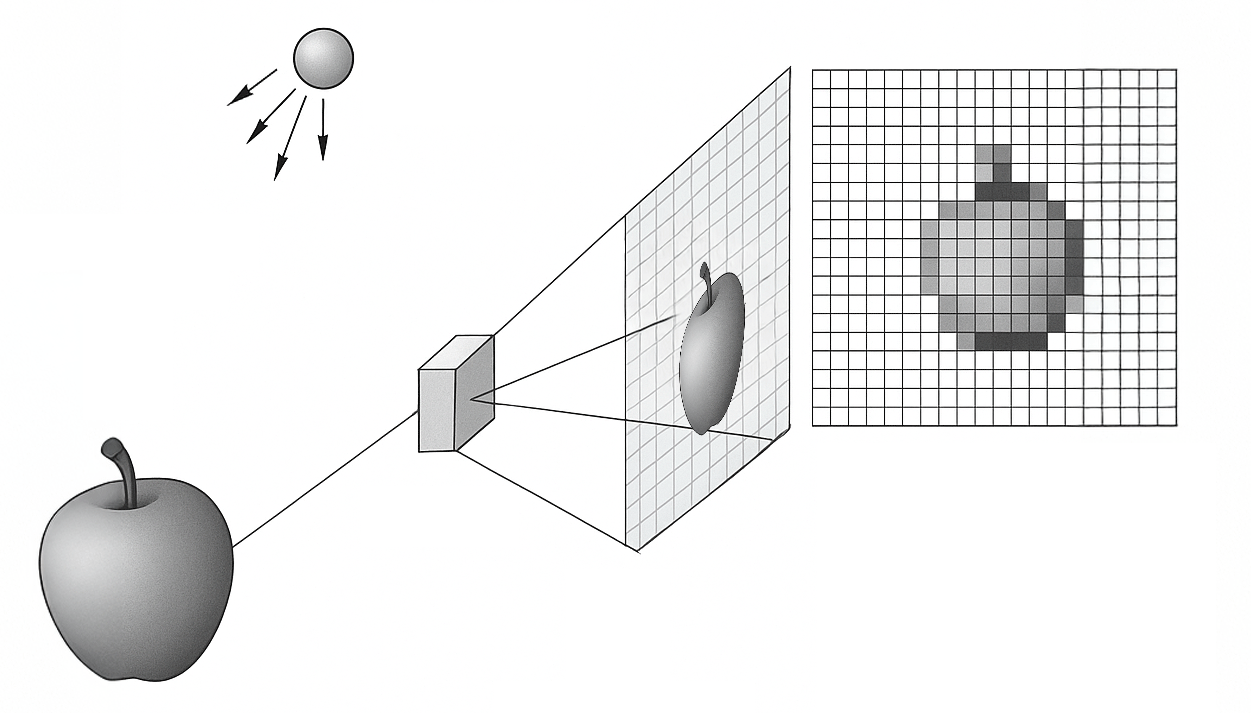
Imagine uma fotografia como uma pintura infinita, onde cada ponto no plano da imagem tem uma intensidade de luz. Essa intensidade é descrita por uma função contínua definida como:

$f: \mathbb{R}^2 \rightarrow \mathbb{R},$

onde $f(x, y)$ representa o nível de cinza (ou brilho) no ponto $(x, y)$ . No mundo real, $x$ e $y$ podem assumir qualquer valor real, mas um computador precisa de uma representação finita: uma grade de pontos discretos.

Amostragem: Discretização da imagem no domínio espacial 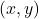$(x, y)$

A amostragem espacial é o processo de selecionar valores dessa função em uma malha regular, definida por intervalos $\Delta x$ e $\Delta y$ . O resultado é uma matriz $M = (m_{ij})$ de dimensões $W \times H$ , onde $W$ é a largura e $H$ é a altura em pixels. Cada elemento da matriz é dado por:

$m_{ij} = f(x_0 + i \cdot \Delta x, y_0 + j \cdot \Delta y)$

Pense nisso como colocar uma tela quadriculada sobre a pintura: cada quadrado (pixel) captura o valor médio de $f$ naquele ponto.

A resolução espacial depende da densidade dessa grade, medida em pixels por unidade de distância (como DPI, ou pontos por polegada). Menores valores de $\Delta x$ e $\Delta y$ significam mais pixels, capturando detalhes mais finos, como os contornos de uma folha em uma fotografia.

$\text{Imagem contínua: } f(x, y) \quad \rightarrow \quad \text{Imagem digital: } \begin{bmatrix} m_{00} & m_{01} & \cdots & m_{0, W-1} \\ m_{10} & m_{11} & \cdots & m_{1, W-1} \\ \vdots & \vdots & \ddots & \vdots \\ m_{H-1, 0} & m_{H-1, 1} & \cdots & m_{H-1, W-1} \end{bmatrix}.$

Por exemplo, uma imagem Full HD ( $1920 \times 1080$ pixels) tem maior resolução espacial do que uma imagem VGA ( $640 \times 480$ pixels), assumindo a mesma área física. A amostragem espacial pode ser visualizada como a transformação de uma função contínua em uma matriz discreta, como mostrado acima.

Quantização: Discretização dos níveis de intensidade

Com a grade de pontos definida, o próximo passo é discretizar os valores de intensidade. No mundo real, esses valores são contínuos, mas um computador exige um número finito de níveis. Esse processo, chamado quantização de intensidade, é realizado por uma função de quantização:

$q: \mathbb{R} \rightarrow \{0, 1, \ldots, L-1\},$

onde $L$ é o número de níveis de intensidade. Para imagens em escala de cinza, é comum usar 1 byte (8 bits) por pixel, resultando em $L = 2^8 = 256$ níveis, com 0 representando preto e 255 representando branco.

Imagine a intensidade como a altura de uma onda em cada pixel. A quantização é como medir essa altura com uma régua que tem apenas $L$ marcações. A função $q$ mapeia cada valor real para o nível discreto mais próximo, criando uma representação em forma de escada. Assim, o valor do pixel na posição $(i, j)$ é:

$m_{ij} = q(f(x_0 + i \cdot \Delta x, y_0 + j \cdot \Delta y)).$

Resolução de Intensidade

A resolução de intensidade, determinada por $L$ , afeta a qualidade visual. Com $L = 256$ (8 bits), as transições de brilho são suaves, ideais para fotos comuns. Porém, com $L = 16$ (4 bits), surgem artefatos como o efeito de “banding”, onde faixas de cor ficam visíveis.

Em aplicações médicas, como tomografias, usam-se 10 a 12 bits ( $L = 1024$ ou $4096$ ) para maior fidelidade.

Para processamento numérico, os valores podem ser normalizados para o intervalo $[0, 1]$ por uma transformação afim $f \leftarrow a f + b$ , e requantizados para armazenamento.

Estrutura Discreta e Implicações Computacionais

A amostragem espacial e a quantização de intensidade convertem uma imagem contínua em uma matriz de inteiros, onde cada $m_{ij}$ representa a intensidade de um pixel.

Essa estrutura discreta é a base do processamento digital e impõe limitações práticas. O espaço necessário para armazenar uma imagem é dado por:

$b = W \cdot H \cdot k, \quad \text{com } k = \log_2(L).$

Ou seja, para uma imagem Full HD ( $1920 \times 1080$ ) com $L = 256$ ( $k = 8$ bits), temos:

$b = 1920 \cdot 1080 \cdot 8 = 16.588.800 \text{ bits} \approx 2 \text{ MB}.$

Isso justifica o uso de compressão (como JPEG), que reduz o tamanho final explorando padrões redundantes sem grande perda visual.

Tanto a resolução espacial ( $W \times H$ ) quanto a intensidade ( $L$ ) afetam algoritmos de visão computacional. Mais pixels aumentam o nível de detalhe e o custo computacional; mais bits por pixel melhoram a precisão, mas exigem mais memória.

Amostragem e Quantização na prática com Python

Agora, vamos explorar dois exemplos práticos para entender como sinais contínuos são transformados em representações digitais. Primeiro, simularemos um sinal unidimensional (1D), como o som de um instrumento musical. Em seguida, aplicaremos os mesmos conceitos a uma imagem real em tons de cinza.

Exemplo 1: Amostragem e Quantização de um Sinal 1D

Imagine que você está gravando o som de um violão. A vibração das cordas cria uma onda sonora contínua, mas para transformá-la em um arquivo digital, precisamos amostrar no tempo e quantizar a amplitude.

Vamos simular isso com um sinal sintético – uma combinação de senoides que mimetiza variações complexas, como uma nota musical. Dividiremos este exemplo em três partes: geração do sinal, amostragem e quantização.

Parte 1: Gerando o Sinal Contínuo

Primeiro, criamos um sinal analógico combinando três senoides com frequências diferentes. Isso simula um sinal complexo, como uma onda sonora ou um padrão de luz.

# Importando bibliotecas necessárias
import numpy as np
import matplotlib.pyplot as plt

# Gerando um sinal contínuo (combinação de senoides)
x = np.linspace(0, 4*np.pi, 1000)
y = np.sin(x) + 0.3 * np.sin(3*x) + 0.2 * np.cos(7*x)

O que está acontecendo aqui?

Usamos np.linspace para criar 1000 pontos entre $0$ e $4\pi$ , “simulando” o domínio contínuo (como o tempo).
O sinal 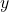$y$ é uma soma de senoides ( 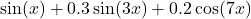$\sin(x) + 0{.}3\sin(3x) + 0{.}2\cos(7x)$ ), criando variações suaves e abruptas, como em um sinal real.
O gráfico mostra a onda contínua, que é o que um sensor (como um microfone) captaria antes da digitalização.

Parte 2: Amostragem do Sinal

Agora, amostramos o sinal em intervalos regulares, simulando o que um sensor faz ao capturar valores em pontos discretos.

# Amostragem: discretização do domínio contínuo
sample_factor = 20
x_sampled = x[::sample_factor]
y_sampled = y[::sample_factor]

O que está acontecendo aqui?

O sample_factor = 20 reduz o sinal a 1/20 dos pontos originais, pegando 1 ponto a cada 20.
x[::sample_factor] e y[::sample_factor] selecionam pontos espaçados regularmente, simulando a amostragem espacial ou temporal.
O gráfico mostra as amostras (pontos vermelhos) sobre o sinal contínuo, destacando a discretização do domínio.

Parte 3: Quantização do Sinal Amostrado

Finalmente, quantizamos os valores amostrados, limitando a amplitude a 8 níveis discretos, como um conversor analógico-digital faria.

# Quantização: redução da resolução em amplitude
num_levels = 8
y_min, y_max = y.min(), y.max()
step = (y_max - y_min) / num_levels
y_quantized = np.floor((y_sampled - y_min) / step) * step + y_min

# Plotando o sinal com amostragem e quantização
plt.figure(figsize=(10, 4))
plt.plot(x, y, label='Sinal Contínuo', alpha=0.75, color='blue')
markerline, stemlines, baseline = plt.stem(x_sampled, y_sampled,
                                          linefmt='r-', markerfmt='ro', basefmt=' ',
                                          label='Amostras')
plt.setp(markerline, alpha=0.2)
plt.setp(stemlines, alpha=0.2)

# Linhas horizontais de quantização
for i in range(num_levels + 1):
    y_line = y_min + i * step
    plt.axhline(y_line, color='gray', linestyle='--', linewidth=0.5, alpha=0.6)

# Linhas verticais de amostragem
for x_tick in x_sampled:
    plt.axvline(x_tick, color='gray', linestyle='--', linewidth=0.5, alpha=0.6)

# Casas de quantização com preenchimento
delta_x = (x[1] - x[0]) * sample_factor
for xi, yi in zip(x_sampled, y_quantized):
    plt.gca().add_patch(plt.Rectangle(
        (xi - delta_x / 2, yi),
        width=delta_x,
        height=step,
        edgecolor='black',
        facecolor='lightgreen',
        linewidth=1.5,
        alpha=0.85
    ))

# Pontos quantizados
plt.scatter(x_sampled, y_quantized, color='green', label='Quantizado')
plt.title("Sinal Amostrado e Quantizado (8 Níveis)")
plt.xlabel("Tempo")
plt.ylabel("Amplitude")
plt.legend()
plt.grid(False)
plt.tight_layout()
plt.show()

O que está acontecendo aqui?

Calculamos o intervalo de quantização (step) dividindo a amplitude total (y_max - y_min) por num_levels = 8.
A função np.floor mapeia cada valor amostrado para o nível quantizado mais próximo.
Retângulos verdes destacam as “caixas” de quantização, mostrando como valores contínuos são aproximados por níveis discretos.
O gráfico final combina o sinal contínuo, as amostras e os valores quantizados, ilustrando a perda de fidelidade.

Dica prática: Tente mudar sample_factor para 10 (mais amostras) ou num_levels para 4 (menos níveis) e observe como o sinal fica mais ou menos fiel ao original.

Exemplo 2: Amostragem e Quantização de uma Imagem Real

Agora, vamos aplicar amostragem e quantização a uma imagem real, como uma foto que você tiraria com seu celular. Aqui, a amostragem espacial define a resolução (quantidade de pixels), e a quantização de intensidade determina os tons de cinza.

Parte 1: Carregando a Imagem em Tons de Cinza

Primeiro, carregamos uma imagem e a convertemos para tons de cinza, transformando-a em uma matriz NumPy.

# Importando bibliotecas necessárias
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
from pathlib import Path

# Caminho base para imagens
NOTEBOOK_DIR = Path.cwd()
IMAGE_DIR = NOTEBOOK_DIR.parent / "images"

# Carregando imagem em tons de cinza
img = Image.open(IMAGE_DIR / 'hexapod.jpg').convert('L')
img_np = np.array(img)

# Exibindo imagem original
plt.figure(figsize=(6, 4))
plt.imshow(img_np, cmap='gray')
plt.title("Imagem Original em Tons de Cinza")
plt.axis('off')
plt.show()

**Foto minha com o hexapod, utilizada para demonstrar os conceitos de amostragem e quantização em imagens digitais.**

O que está acontecendo aqui?

Usamos PIL.Image.open para carregar a imagem hexapod.jpg e .convert('L') para transformá-la em tons de cinza (valores de 0 a 255).
Convertemos a imagem em uma matriz NumPy (img_np) para manipulação numérica.
O gráfico mostra a imagem original, que representa uma cena contínua antes da manipulação.

Parte 2: Amostragem Espacial da Imagem

Reduzimos a resolução da imagem, simulando uma câmera com menos pixels.

# Amostragem espacial com fator 4
sampling_factor = 4
img_sampled = img_np[::sampling_factor, ::sampling_factor]

# Exibindo imagem amostrada
plt.figure(figsize=(6, 4))
plt.imshow(img_sampled, cmap='gray', interpolation='nearest')
plt.title("Imagem com Amostragem Espacial (fator 4)")
plt.axis('off')
plt.show()

O que está acontecendo aqui?

O sampling_factor = 4 reduz a resolução, pegando 1 pixel a cada 4 em ambas as dimensões (largura e altura).
img_np[::sampling_factor, ::sampling_factor] seleciona uma submatriz, diminuindo o número de pixels.
O resultado é uma imagem mais “pixelada”, com menos detalhes, como se fosse capturada por uma câmera de baixa resolução.

Parte 3: Quantização de Intensidade da Imagem

Agora, quantizamos os valores da imagem amostrada, reduzindo os tons de cinza para 8 e depois para 2 níveis.

# Função de quantização uniforme
def quantize_image(image, levels):
    image_min = image.min()
    image_max = image.max()
    step = (image_max - image_min) / levels
    return np.floor((image - image_min) / step) * step + image_min

# Quantizando a imagem amostrada (8 níveis)
quantization_levels = 8
img_quantized_8 = quantize_image(img_sampled, quantization_levels)

# Exibindo imagem amostrada e quantizada (8 níveis)
plt.figure(figsize=(6, 4))
plt.imshow(img_quantized_8, cmap='gray', interpolation='nearest')
plt.title("Imagem Amostrada + Quantizada (8 Níveis)")
plt.axis('off')
plt.show()

# Quantizando a imagem amostrada (2 níveis)
quantization_levels = 2
img_quantized_2 = quantize_image(img_sampled, quantization_levels)

# Exibindo imagem amostrada e quantizada (2 níveis)
plt.figure(figsize=(6, 4))
plt.imshow(img_quantized_2, cmap='gray', interpolation='nearest')
plt.title("Imagem Amostrada + Quantizada (2 Níveis)")
plt.axis('off')
plt.show()

O que está acontecendo aqui?

A função quantize_image mapeia os valores de intensidade para levels discretos, calculando o intervalo (step) e arredondando com np.floor.
Com 8 níveis, a imagem mantém alguma fidelidade, mas perde transições suaves de tons.
Com 2 níveis, a imagem vira binária (preto e branco), mostrando o efeito extremo da quantização.
Os gráficos mostram como a redução de níveis cria artefatos visuais, como o “banding”.

Dica prática: Experimente mudar sampling_factor para 8 ou quantization_levels para 16 e veja como a imagem ganha ou perde qualidade.

Takeaways

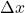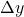Amostragem espacial transforma uma imagem contínua em uma matriz de pixels, definida por uma grade de intervalos $\Delta x$ e $\Delta y$ . A densidade dessa grade (resolução espacial) determina a quantidade de detalhes capturados.
Quantização de intensidade reduz os valores contínuos de brilho para um conjunto finito de níveis ( 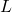$L$ ). Menor 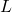$L$ (como 2 ou 8 níveis) causa perda de detalhes, mas pode ser útil em aplicações específicas, como binarização.
A combinação de amostragem e quantização define a estrutura de uma imagem digital, impactando diretamente o tamanho do arquivo ( 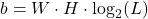$b = W \cdot H \cdot \log_2(L)$ ) e o desempenho de algoritmos de visão computacional.
Em aplicações práticas, como câmeras digitais ou imagens médicas, o equilíbrio entre resolução espacial e de intensidade é crucial para otimizar qualidade e eficiência computacional.
Os exemplos em Python ilustram como amostragem e quantização alteram visualmente uma imagem, desde a preservação de detalhes com 8 níveis até a simplificação extrema com 2 níveis.