Entender as transformações de matriz e sistemas de coordenadas é essencial para converter com precisão objetos 3D em imagens 2D. Esse processo, amplamente utilizado em aplicações como videogames, realidade virtual e realidade aumentada, permite renderização realista de imagens mapeando pontos 3D no mundo para pontos 2D em um plano de imagem.
Neste tutorial, exploraremos as complexidades das transformações de matriz e sistemas de coordenadas, focando na geometria da imagem da câmera, coordenadas de imagem e do mundo. Incluiremos uma implementação em Python para ajudar a ilustrar esses conceitos, com foco em como manipular a câmera e obter suas coordenadas.
Geometria da Formação de Imagens
Para compreender a formação de uma imagem a partir de um ponto 3D no espaço, precisamos entender o processo do ponto de vista da geometria e álgebra linear. Essencialmente, precisamos projetar um ponto 3D em um plano de imagem 2D usando um processo chamado projeção em perspectiva.
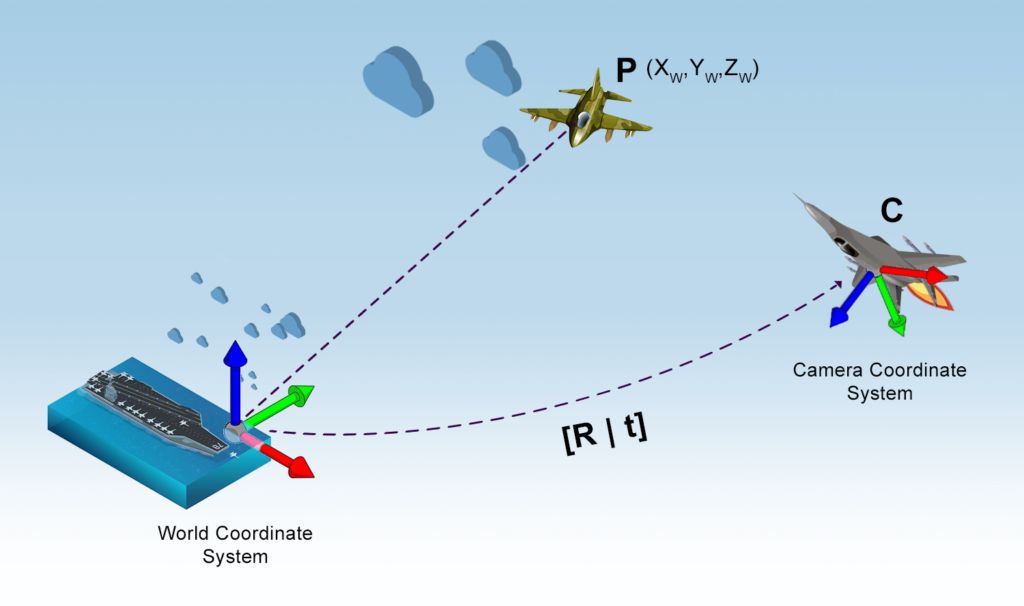
Isso envolve levar em consideração três componentes críticos: o Sistema de Coordenadas do Mundo, o Sistema de Coordenadas da Câmera e o Plano de Imagem. Para transformar de coordenadas do Mundo para coordenadas de Pixel, realizamos as seguintes três etapas:
- Transformar o ponto do mundo
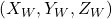com centro óptico 
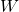para um novo sistema de coordenadas com o centro óptico da câmera 
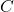como a origem 
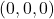. Isso é feito usando uma transformação de corpo rígido, composta por rotação 
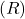e translação 
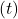. - Projetar o ponto da câmera
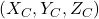no sensor óptico, criando novas coordenadas 
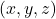no mesmo sistema de coordenadas. Isso é alcançado usando a matriz de parâmetros intrínsecos da câmera 
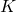. O sensor óptico é frequentemente referido como o “plano de imagem” ou “quadro de imagem”. - Normalizar 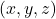para coordenadas de pixel
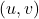dividindo por 
e ajustando a origem da imagem.
Ao entender e aplicar essas etapas, podemos efetivamente converter um ponto 3D do Sistema de Coordenadas do Mundo para coordenadas de pixel em uma imagem, o que é essencial no campo da visão computacional e formação de imagem.
Sistema de Coordenadas do Mundo
Imagine que você seja um piloto de elite, Maverick, participando de um combate aéreo de alto risco contra uma aeronave inimiga. Para descrever a posição dos objetos no espaço aéreo, você precisa estabelecer um sistema de coordenadas para o mundo 3D em que está voando.
Esse processo envolve dois componentes principais:
- Origem: podemos escolher arbitrariamente qualquer ponto no mundo 3D como a origem, como o porta-aviões da marinha, representado pelas coordenadas .
- Eixos X, Y, Z: em seguida, definimos os eixos X, Y e Z com base em uma referência fixa, como o eixo longitudinal do porta-aviões, o eixo lateral e a linha vertical apontando para o céu a partir das metralhadoras.
Com nosso sistema de coordenadas no lugar, podemos determinar as coordenadas 3D de qualquer ponto 
dentro do espaço aéreo, medindo sua distância da origem ao longo dos eixos X, Y e Z. Este sistema de coordenadas é conhecido como Sistema de Coordenadas do Mundo.
Sistema de Coordenadas da Câmera
Agora, imagine o Maverick rasgando os céus além das linhas inimigas em seu F-18 Super Hornet, navegando habilmente em todos os eixos para se envolver e travar em uma aeronave alvo. O objetivo do Maverick é estabelecer uma linha de visão com a aeronave inimiga, fazendo com que ela apareça em sua tela Heads-Up Display (HUD).
Para fins educacionais, vamos considerar a aeronave e seu piloto como uma câmera. A imagem da aeronave inimiga deve ser capturada por esta câmera, então estamos interessados no sistema de coordenadas 3D anexado a ele, conhecido como sistema de coordenadas da câmera. Nesse cenário, precisamos encontrar a relação entre as coordenadas do mundo 3D e as coordenadas da câmera 3D.
Se colocássemos a câmera na origem das coordenadas do mundo e alinhássemos seus eixos X, Y e Z com os eixos do mundo, os dois sistemas de coordenadas seriam idênticos. No entanto, essa é uma restrição impraticável. Queremos que a câmera esteja em qualquer lugar do mundo e possa olhar em qualquer direção. Nesse caso, precisamos encontrar a relação entre as coordenadas 3D do mundo e as coordenadas 3D da câmera ‘Maverick’.
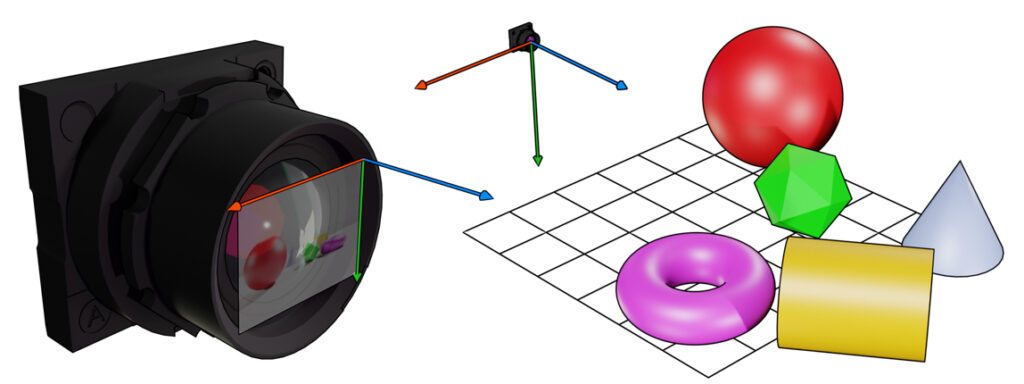
Suponha que a aeronave de Maverick esteja em um local arbitrário 
no espaço aéreo. A coordenada da câmera é transladada por em relação às coordenadas do mundo. Além disso, a aeronave pode olhar em qualquer direção, ou seja, está girada em relação ao sistema de coordenadas do mundo.
Em 3D, a rotação é capturada usando três parâmetros – guinada, arfagem e rolagem. Eles também podem ser representados como um eixo em 3D (dois parâmetros) e uma rotação angular em torno desse eixo (um parâmetro). Para manipulação matemática, geralmente é mais conveniente codificar a rotação como uma matriz 3×3. Embora uma matriz 3×3 tenha nove elementos, uma matriz de rotação possui apenas três graus de liberdade devido às restrições de rotação.
Com essas informações, podemos estabelecer a relação entre o Sistema de Coordenadas do Mundo e o Sistema de Coordenadas da Câmera usando uma matriz de rotação R e um vetor de translação de 3 elementos 
.
Isso significa que o ponto P, que tinha valores de coordenadas nas coordenadas do mundo, terá valores de coordenadas diferentes no sistema de coordenadas da câmera. As duas coordenadas estão relacionadas pela seguinte equação:
![\[ \begin{bmatrix} X_C \\ Y_C \\ Z_C \end{bmatrix} = \mathbf{R} \begin{bmatrix} X_W \\ Y_W \\ Z_W \end{bmatrix} + \mathbf{t} \]](https://sigmoidal.ai/wp-content/ql-cache/quicklatex.com-f93937bd6693410965950987174e9894_l3.png "Rendered by QuickLaTeX.com")
Representando a rotação como uma matriz, podemos simplificar a rotação com multiplicação de matrizes em vez de manipulação de símbolos tediosa exigida em outras representações como guinada, arfagem e rolagem. Isso deve ajudá-lo a entender por que representamos rotações como uma matriz. Às vezes, a expressão acima é escrita de forma mais compacta. O vetor de translação 3×1 é anexado como uma coluna no final da matriz de rotação 3×3 para obter uma matriz 3×4 chamada Matriz Extrínseca:
![\[ \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = P \begin{bmatrix} X_C \\ Y_C \\ Z_C \\ 1 \end{bmatrix} \]](https://sigmoidal.ai/wp-content/ql-cache/quicklatex.com-7c88dba908765ae0eee12e1e51a800f1_l3.png "Rendered by QuickLaTeX.com")
onde a matriz de projeção da câmera P é dada por:
![\[ P = K \begin{bmatrix} R \ | \ t \end{bmatrix} \]](https://sigmoidal.ai/wp-content/ql-cache/quicklatex.com-344e7d97081aae6a01f8bdf3ab6aa698_l3.png "Rendered by QuickLaTeX.com")
Sistema de Coordenadas da Imagem
Neste combate aéreo de alto risco, Maverick deve trazer a aeronave inimiga para seu Head-Up Display (HUD) para travar no alvo e estabelecer uma solução de disparo. Analogamente, precisamos projetar um ponto 3D do sistema de coordenadas da câmera no plano da imagem. O plano da imagem, um plano 2D que representa o campo de visão da câmera, é onde nosso mundo 3D é projetado para formar uma imagem 2D.
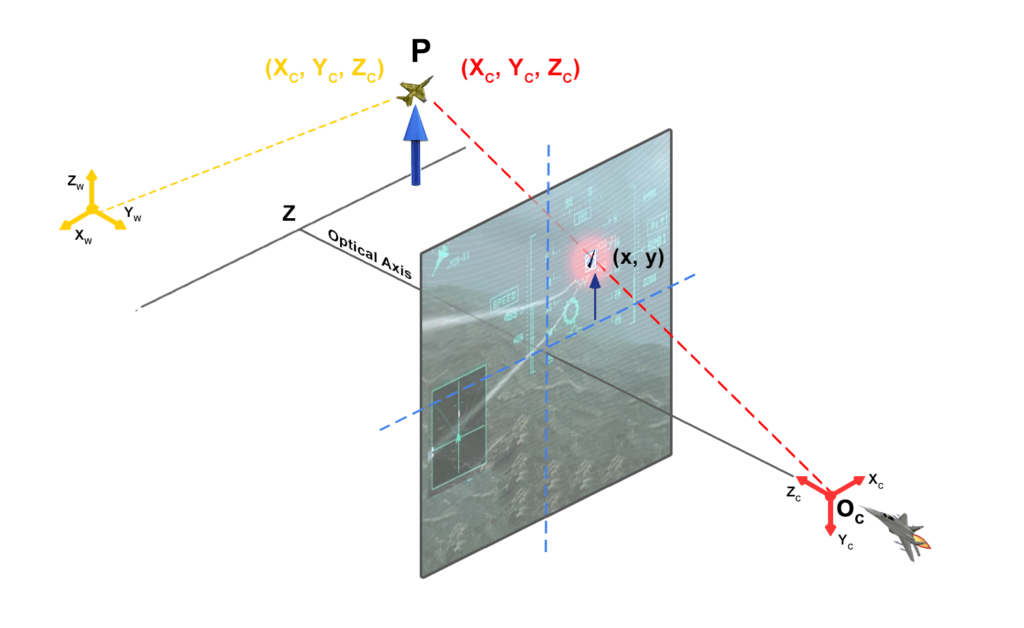
O Sistema de Coordenadas de Imagem tem sua origem no canto inferior esquerdo do plano de imagem, com os eixos X e Y se estendendo à direita e para cima, respectivamente. Normalmente, as unidades de medida são em pixels, começando na origem (0, 0) e atingindo as coordenadas máximas de acordo com a largura e altura da imagem.
Para projetar um ponto 3D do sistema de coordenadas da câmera no plano da imagem, primeiro precisamos estabelecer a relação entre os parâmetros intrínsecos da câmera e o Sistema de Coordenadas de Imagem. Os parâmetros intrínsecos incluem a distância focal (f) e o ponto principal 
, que representa o centro do plano da imagem.
A matriz de parâmetros intrínsecos da câmera, denotada como K, é definida como:
![\[ K = \begin{bmatrix} f & 0 & u_0 \\ 0 & f & v_0 \\ 0 & 0 & 1 \end{bmatrix} \]](https://sigmoidal.ai/wp-content/ql-cache/quicklatex.com-5f1c508a4cb6d0013c7e2c7ed4e2cd5d_l3.png "Rendered by QuickLaTeX.com")
Agora que temos a matriz de parâmetros intrínsecos, podemos projetar um ponto 3D do sistema de coordenadas da câmera no plano da imagem usando a seguinte equação:
![\[ \begin{bmatrix} x \\ y \\ z \end{bmatrix} = K \begin{bmatrix} X_C \\ Y_C \\ Z_C \end{bmatrix} \]](https://sigmoidal.ai/wp-content/ql-cache/quicklatex.com-8686b85a7f4e821ee777d20f343410cc_l3.png "Rendered by QuickLaTeX.com")
Finalmente, normalizamos o ponto projetado (x, y, z) para obter as coordenadas de pixel correspondentes no plano da imagem:
![\[ u = \frac{x}{z} \quad \text{and} \quad v = \frac{y}{z} \]](https://sigmoidal.ai/wp-content/ql-cache/quicklatex.com-fec14e6424f39107cf3ddde7b850501a_l3.png "Rendered by QuickLaTeX.com")
Em um contexto mais geral, projetamos com sucesso um ponto 3D do sistema de coordenadas do mundo para o sistema de coordenadas da imagem, transformando-o em uma imagem 2D. Ao compreender e aplicar os conceitos do Sistema de Coordenadas do Mundo, Sistema de Coordenadas da Câmera e Sistema de Coordenadas de Imagem, podemos converter efetivamente pontos 3D em coordenadas de pixel em uma imagem. Este processo é crucial para várias aplicações em gráficos de computador, como videogames, realidade virtual e realidade aumentada.
Implementação em Python
Na seção “Implementação em Python”, exploraremos como manipular a posição e orientação da câmera em um espaço 3D usando Python. Usaremos os conceitos de projeção de câmera e geometria de formação de imagens para criar uma implementação em Python que demonstre a relação entre os sistemas de coordenadas do mundo e da câmera.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.linalg import expm
class Camera:
def __init__(self, P):
self.P = P
self.K = None
self.R = None
self.t = None
self.c = None
def translate(self, translation_vector):
T = np.eye(4)
T[:3, 3] = translation_vector
self.P = np.dot(self.P, T)
def rotate(self, rotation_vector):
R = rotation_matrix(rotation_vector)
self.P = np.dot(self.P, R)
def position(self):
return self.P[:3, 3]
def rotation_matrix(a):
R = np.eye(4)
R[:3, :3] = expm(np.array([[0, -a[2], a[1]], [a[2], 0, -a[0]], [-a[1], a[0], 0]]))
return R
Este trecho de código ilustra uma implementação em Python de uma classe Camera que pode ser usada para realizar translações e rotações em uma matriz de projeção 3D. A classe Camera tem métodos para transladar e rotacionar a câmera, e um método position que retorna a posição da câmera. A função rotation_matrix é usada para criar uma matriz de rotação a partir de um vetor de rotação, que é então usado para atualizar a matriz de projeção. As bibliotecas numpy e scipy são usadas para realizar operações matriciais e calcular a exponencial de uma matriz, respectivamente. A biblioteca matplotlib é usada para visualizar a projeção 3D.
def draw_axis(ax, position, label, color):
x_arrow = np.array([1, 0, 0])
y_arrow = np.array([0, 1, 0])
z_arrow = np.array([0, 0, 1])
ax.quiver(*position, *x_arrow, color=color, arrow_length_ratio=0.1)
ax.quiver(*position, *y_arrow, color=color, arrow_length_ratio=0.1)
ax.quiver(*position, *z_arrow, color=color, arrow_length_ratio=0.1)
ax.text(*(position + x_arrow), f"{label}_x")
ax.text(*(position + y_arrow), f"{label}_y")
ax.text(*(position + z_arrow), f"{label}_z")
def plot_world_and_camera(world_coordinates, camera):
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')
world_x, world_y, world_z = zip(world_coordinates)
ax.scatter(world_x, world_y, world_z, c='b', marker='o', label='World Coordinates', s=54)
camera_x, camera_y, camera_z = camera.position()
ax.scatter(camera_x, camera_y, camera_z, c='r', marker='^', label='Camera Position', s=54)
draw_axis(ax, camera.position(), "C", color="red")
draw_axis(ax, world_origin, "W", color="blue")
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_xlim(-3, 3)
ax.set_ylim(-3, 3)
ax.set_zlim(-3, 3)
ax.legend()
plt.show()
Este trecho de código demonstra a função plot_world_and_camera, que é usada para plotar as coordenadas do mundo e a posição da câmera em um espaço 3D. A função recebe os objetos world_coordinates e camera como argumentos e cria um gráfico de dispersão 3D usando a biblioteca matplotlib. A função draw_axis é usada para desenhar os eixos x, y e z tanto para os sistemas de coordenadas do mundo quanto da câmera. O método camera.position() é usado para obter a posição da câmera no sistema de coordenadas do mundo. Os métodos ax.set_xlabel, ax.set_ylabel e ax.set_zlabel são usados para rotular os eixos x, y e z, respectivamente. Por fim, os métodos ax.legend() e plt.show() são usados para exibir a legenda e o gráfico, respectivamente.
world_origin = (1, 1, 1) # Set up Camera P = np.hstack((np.eye(3), np.array([[0], [0], [0]]))) cam = Camera(P) # Plot the World and Camera Coordinate Systems plot_world_and_camera(world_origin, cam)
Como demonstrado no trecho de código acima, a variável world_origin é inicializada com as coordenadas (1, 1, 1). A variável P é inicializada como uma matriz identidade 3×4, que representa a matriz de projeção da câmera. A classe Camera é então inicializada com a matriz P. Por fim, a função plot_world_and_camera é chamada com os objetos world_origin e cam como argumentos para plotar as coordenadas do mundo e a posição da câmera em um espaço 3D.
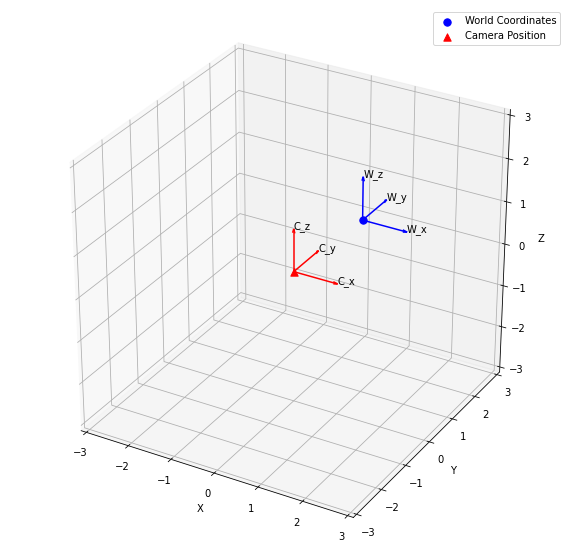
Agora, moveremos a câmera aplicando uma translação e uma rotação. Inicializamos o vetor de translação como [1, 1, 1] e o eixo de rotação como [0, 0, 1]. Em seguida, definimos o ângulo de rotação como np.pi / 4. Em seguida, criamos um vetor de rotação multiplicando o eixo de rotação pelo ângulo de rotação. Por fim, aplicamos a translação e a rotação à câmera usando os métodos translate e rotate, respectivamente. Depois disso, plotamos os sistemas de coordenadas do mundo e da câmera atualizados usando a função plot_world_and_camera.
# Move the Camera translation_vector = np.array([1, 1, 1]) rotation_axis = np.array([0, 0, 1]) rotation_angle = np.radians(45) rotation_vector = rotation_axis * rotation_angle cam.translate(translation_vector) cam.rotate(rotation_vector) ## Plot the World and Camera Coordinate Systems after moving the Camera plot_world_and_camera(world_origin, cam)
Ao executar este trecho de código, você poderá visualizar as posições atualizadas dos sistemas de coordenadas da câmera e do mundo após a aplicação da translação e da rotação na câmera. Isso ajudará você a entender como a matriz de projeção da câmera muda à medida que a câmera se move no espaço 3D.
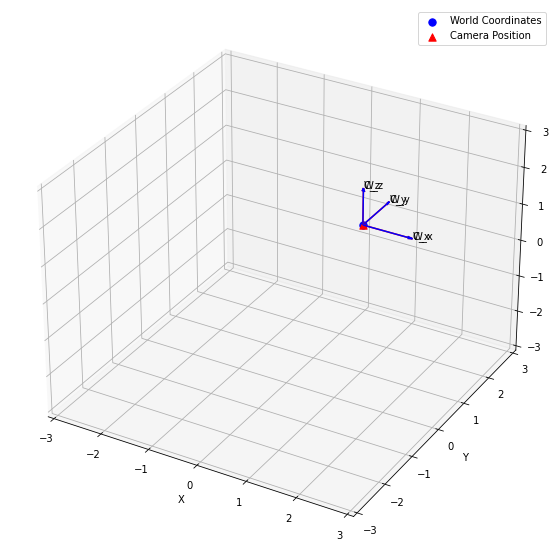
Assim, demonstramos como manipular a posição e a orientação da câmera em um espaço 3D usando Python, implementando os conceitos de projeção da câmera e geometria de imagem. Também fornecemos uma implementação em Python da classe Camera, que pode ser usada para realizar translações e rotações em uma matriz de projeção 3D. Ao entender e aplicar esses conceitos, você poderá criar e manipular câmeras virtuais em um espaço 3D, o que é crucial para várias aplicações em computação gráfica, como jogos de vídeo, realidade virtual e realidade aumentada.
Conclusão
Aqui estão algumas informações principais que você deve lembrar deste tutorial:
- A projeção 3D é o processo de transformar pontos 3D em pontos 2D em um plano.
- O modelo da câmera define a relação entre o mundo 3D e a imagem 2D capturada pela câmera.
- A matriz de projeção da câmera é uma matriz 3×4 que mapeia pontos 3D para pontos 2D no plano da imagem.
- Python fornece bibliotecas poderosas como NumPy e Matplotlib para implementar projeção 3D e modelo de câmera.
Em nosso próximo artigo, construiremos sobre esta base e demonstraremos como renderizar objetos 3D e projetá-los no espaço de pixel, criando efetivamente imagens 2D realistas a partir de cenas 3D. No final do próximo post, você não apenas terá uma compreensão sólida dos princípios subjacentes da projeção da câmera, mas também as habilidades práticas para aplicar esse conhecimento em seus projetos. Fique atento para esta emocionante continuação e junte-se a nós enquanto desvendamos os segredos da projeção da câmera em gráficos de computador.
