Fundamentos da Formação da Imagem

Em um mundo repleto de mistérios e maravilhas, a fotografia se ergue como um fenômeno que captura o efêmero e o eterno em um único instante. Como uma dança silenciosa entre luz e sombra, ela convida nossa imaginação a vagar pelos corredores do tempo e do espaço. Através de um processo surpreendentemente simples, a captura de raios de luz por meio de uma abertura e um tempo de exposição, somos levados à contemplação de fotografias que sabemos que ficarão eternizadas.

O filósofo José Ortega y Gasset uma vez refletiu sobre a paixão pela verdade como sendo a mais nobre e inexorável. E, sem dúvida, a fotografia é uma das mais sublimes expressões dessa busca pela verdade, capturando a realidade em um fragmento de tempo.

E por trás desse processo, está a magia das matrizes, projeções, transformações de coordenadas e modelos matemáticos que, como fios invisíveis, tecem a tapeçaria entre a realidade capturada pela lente de uma câmera e os pixels brilhantes na sua tela.

Mas para entender como é possível modelar matematicamente o mundo visual, com toda a sua riqueza de detalhes, nós precisamos antes entender por que a visão é tão complexa e desafiadora. Neste é primeiro artigo da série Visão Computacional: Algoritmos e Aplicações, e eu quero te convidar a conhecer como as máquinas enxergam uma imagem e como uma imagem é formada.

Os desafios da Visão Computacional

A visão computacional é uma área fascinante que busca desenvolver técnicas matemáticas capazes de reproduzir a percepção tridimensional do mundo ao nosso redor. Richard Szeliski, em seu livro “Computer Vision: Algorithms and Applications”, descreve como, com aparente facilidade, percebemos a estrutura tridimensional do mundo ao nosso redor e a riqueza de detalhes que podemos extrair de uma simples imagem. Entretanto, a visão computacional enfrenta dificuldades em reproduzir esse nível de detalhe e precisão.

Szeliski destaca que, apesar do avanço das técnicas de visão computacional nas últimas décadas, ainda não conseguimos fazer com que um computador explique uma imagem com o mesmo nível de detalhe que uma criança de dois anos. A visão é um problema inverso, onde procuramos recuperar informações desconhecidas a partir de dados insuficientes para especificar completamente a solução. Para resolver esse problema, é necessário recorrer a modelos baseados em física e probabilidade, ou aprendizado de máquina com grandes conjuntos de exemplos.

Modelar o mundo visual em toda a sua complexidade é um desafio maior do que, por exemplo, modelar o trato vocal que produz sons falados. A visão computacional busca descrever e reconstruir propriedades como forma, iluminação e distribuição de cores a partir de uma ou mais imagens, algo que humanos e animais fazem com facilidade, enquanto os algoritmos de visão computacional são propensos a erros.

Como uma imagem é formada

Antes de analisarmos e manipularmos imagens, é preciso entender o processo de formação de imagem. Como exemplos de componentes do processo de produção de uma dada imagem, Szeliski (2022) cita:

1. Projeção em perspectiva: A maneira como objetos tridimensionais são projetados em uma imagem bidimensional, levando em conta a posição e a orientação dos objetos em relação à câmera.
2. Dispersão da luz após atingir a superfície: A forma como a luz se espalha depois de interagir com a superfície dos objetos, influenciando a aparência das cores e sombras na imagem.
3. Óptica da lente: O processo pelo qual a luz passa através de uma lente, afetando a formação da imagem devido à refração e outros fenômenos ópticos.
4. Matriz de filtro de cor Bayer: Um padrão de filtro de cor usado na maioria das câmeras digitais para capturar cores em cada pixel, permitindo a reconstrução das cores originais da imagem.

Em relação ao processo de formação da imagem, este é bem simples geometricamente. Um objeto reflete a luz que incide sobre ele, e essa luz é capturada por um sensor, formando uma imagem após um certo tempo de exposição. Mas se fosse assim, dada a grande quantidade de raios de luz vindos a partir tantos ângulos diferentes, o nosso sensor não seria capaz de focar em nada e apresentaria apenas um certo borrão luminoso.

Para garantir que cada parte do cenário incida apenas em um ponto do sensor, é possível introduzir uma barreira óptica com um orifício que permite a passagem apenas uma parte dos raios de luz, reduzindo o desfoque e proporcionando uma imagem mais nítida. Esse buraco colocado na barreira se chama de abertura ou pinhole, e é crucial para a formação de uma imagem nítida, permitindo que câmeras e outros dispositivos de captura de imagem funcionem adequadamente.

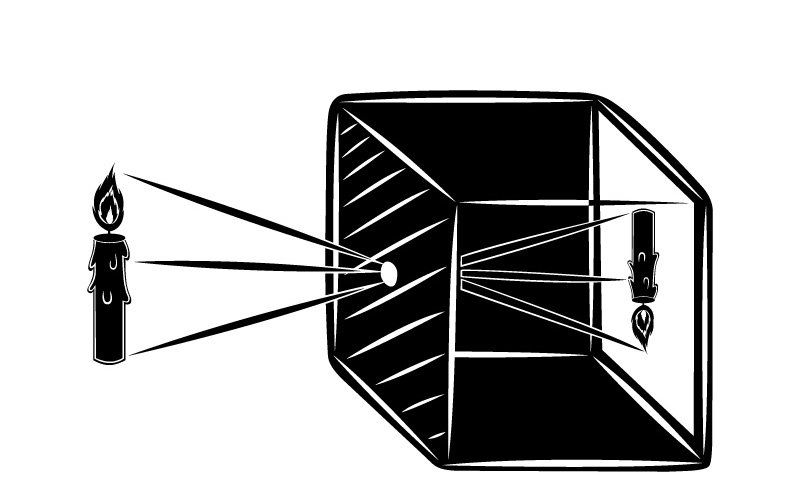
Esse princípio da física, conhecido como câmera escura, serve como base para a construção de qualquer câmera fotográfica. Uma câmera de modelo pinhole ideal possui um orifício infinitamente pequeno para obter uma imagem infinitamente nítida.

No entanto, o problema com as câmeras pinhole é que há uma relação de trade-off entre nitidez e luminosidade. Quanto menor for o orifício, maior será a nitidez da imagem. Porém, como a quantidade de luz que passa é menor, é necessário aumentar o tempo de exposição.

Além disso, se o orifício for da mesma ordem de grandeza do comprimento de onda da luz, teremos o efeito da difração, que acaba distorcendo a imagem. Na prática, um orifício menor que 0,3 mm causará interferências nas ondas de luz, tornando a imagem borrada.

A solução para esse problema é o uso de lentes. No caso, uma lente convergente fina permitirá que o raio que passe pelo centro da lente não seja defletido e que todos os raios paralelos ao eixo óptico se intersectem em um único ponto (ponto focal).

A Magia das Lentes na Formação de Imagens

Lentes são elementos ópticos essenciais na formação de imagens, pois permitem que mais luz seja capturada pelo sensor enquanto ainda mantêm a nitidez da imagem. As lentes funcionam refratando a luz que passa através delas, direcionando os raios de luz para os pontos corretos no sensor.

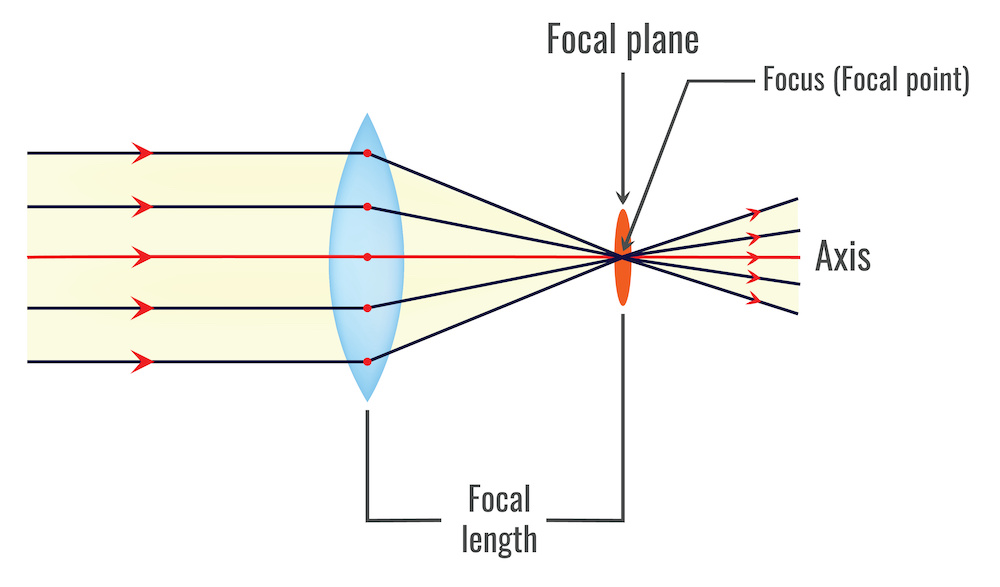
No contexto da calibração de câmera, a lente fina convergente é usada como um modelo simplificado para descrever a relação entre o mundo tridimensional e a imagem bidimensional capturada pelo sensor da câmera. Este modelo teórico é útil para entender os princípios básicos da óptica geométrica e simplificar os cálculos envolvidos na calibração da câmera, e deve satisfazer duas propriedades:

1. Os raios que passam pelo Centro Óptico não são desviados; e
2. Todos os raios paralelos ao Eixo Óptico convergem no Ponto Focal.

Como veremos no próximo artigo, a calibração da câmera envolve a determinação dos parâmetros intrínsecos e extrínsecos que descrevem a relação entre as coordenadas do mundo real e as coordenadas da imagem. Os parâmetros intrínsecos incluem a distância focal, o ponto principal e a distorção da lente, enquanto os parâmetros extrínsecos descrevem a posição e a orientação da câmera em relação ao mundo.

Embora o modelo de lente fina seja uma simplificação do sistema óptico real de uma câmera, ele pode ser usado como ponto de partida para a calibração.

Foco e distância focal

O foco é um dos principais aspectos na formação de imagens com lentes. A distância focal, representada por , é a distância entre o centro da lente e o ponto focal, onde os raios de luz paralelos ao eixo óptico convergem após passar pela lente.

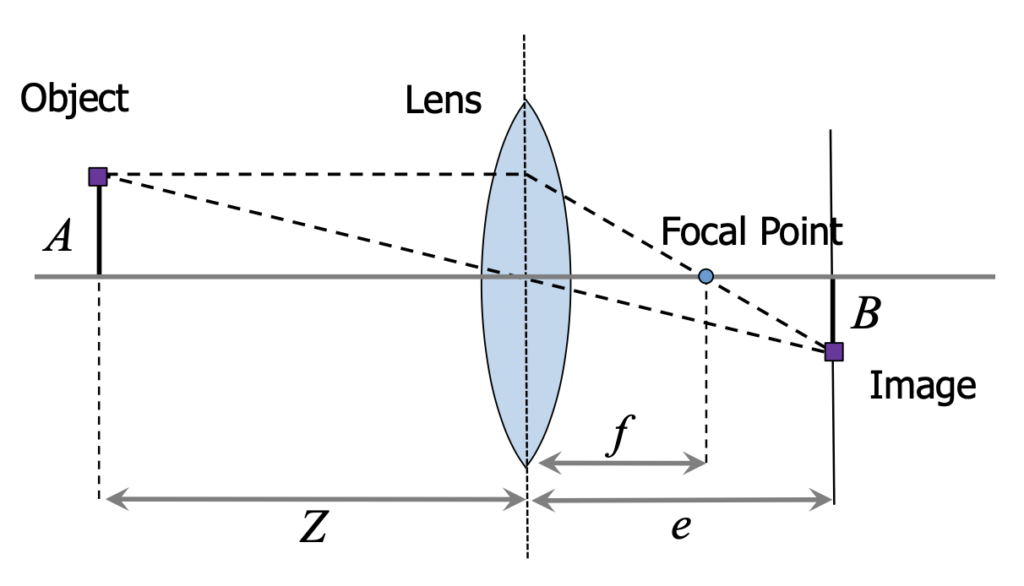
A distância focal está diretamente relacionada à capacidade da lente de concentrar a luz e, consequentemente, influencia a nitidez da imagem.

A equação do foco é dada por:

onde é a distância entre o objeto e a lente, e é a distância entre a imagem formada e a lente. Essa equação descreve a relação entre a distância focal, a distância do objeto e a distância da imagem formada.

Abertura e profundidade de campo

A abertura é outro aspecto fundamental na formação de imagens com lentes. A abertura, geralmente representada por um valor de -número, controla a quantidade de luz que passa através da lente. Um valor de -número menor indica uma abertura maior, permitindo a entrada de mais luz e resultando em imagens mais brilhantes.

A abertura também afeta a profundidade de campo, que é a faixa de distância em que os objetos aparecem nítidos na imagem. Uma abertura maior (menor valor de -número) resulta em uma profundidade de campo menor, fazendo com que apenas os objetos próximos ao plano focal sejam nítidos, enquanto objetos mais distantes ou mais próximos ficam desfocados.

Essa característica pode ser útil para criar efeitos artísticos, como destacar um objeto em primeiro plano e desfocar o fundo.

Distância focal e ângulo de visão

A distância focal da lente também afeta o ângulo de visão, que é a extensão do cenário capturado pela câmera. Lentes com uma distância focal menor têm um ângulo de visão mais amplo, enquanto lentes com uma distância focal maior têm um ângulo de visão mais estreito. Lentes grande angulares, por exemplo, possuem distâncias focais curtas e são capazes de capturar uma ampla visão da cena. Lentes teleobjetivas, por outro lado, possuem distâncias focais longas e são adequadas para capturar objetos distantes com maior detalhamento.

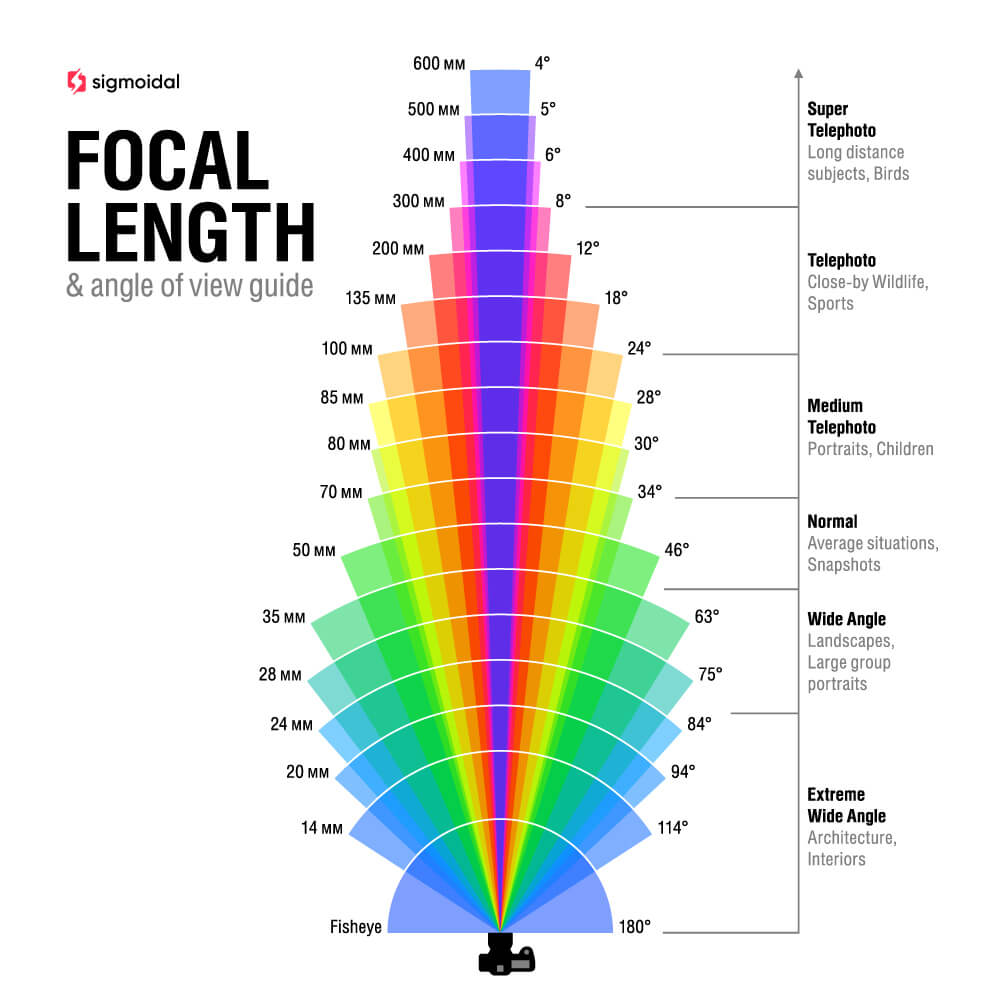
Ao selecionar a lente apropriada, é possível ajustar a composição e o enquadramento da imagem, bem como controlar a quantidade de luz que entra no sensor e a profundidade de campo. Além disso, o uso de lentes permite a manipulação da perspectiva e a captura de detalhes sutis que seriam impossíveis de serem registrados com um modelo pinhole.

Em suma, a lente é um componente crucial na formação de imagens, permitindo que os fotógrafos e cineastas controlem e moldem a luz de maneira eficaz e criativa. Com o conhecimento adequado sobre as características das lentes e suas implicações na formação da imagem, é possível explorar todo o potencial das câmeras e outros dispositivos de captura de imagem, criando imagens verdadeiramente impressionantes e expressivas.

Captura e Representação de Imagens Digitais

As câmeras digitais empregam um conjunto de fotodiodos (CCD ou CMOS) para converter fótons (energia luminosa) em elétrons, diferindo das câmeras analógicas que utilizam filme fotográfico para registrar as imagens. Essa tecnologia permite capturar e armazenar imagens em formato digital, simplificando o processamento e compartilhamento das fotos.

As imagens digitais são organizadas como uma matriz de pixels, onde cada pixel representa a intensidade da luz em um ponto específico da imagem. Um exemplo comum de imagem digital é a imagem de 8 bits, na qual cada pixel possui um valor de intensidade que varia de 0 a 255. Essa faixa de valores é resultado do uso de 8 bits para representar a intensidade, o que permite um total de valores distintos para cada pixel.

Na figura acima, vemos um exemplo de como uma máquina “enxergaria” uma aeronave da Força Aérea Brasileira. Nesse caso, cada pixel possui um vetor de valores associados a cada um dos canais RGB.

As câmeras digitais geralmente adotam um sistema de detecção de cores baseado em imagens RGB, onde cada cor é representada por um canal específico (vermelho, verde e azul). Um dos métodos mais comuns para capturar essas cores é o padrão Bayer, desenvolvido por Bryce Bayer em 1976 enquanto trabalhava na Kodak. O padrão Bayer consiste em uma matriz de filtros RGB alternados colocados sobre o conjunto de pixels.

É interessante notar que a quantidade de filtros verdes é duas vezes maior que a de filtros vermelhos e azuis, pois o sinal de luminância é determinado principalmente pelos valores verdes, e o sistema visual humano é muito mais sensível às diferenças espaciais de luminância do que de crominância. Para cada pixel, os componentes de cor ausentes podem ser estimados a partir dos valores vizinhos por interpolação – um processo conhecido como desmosaicagem.

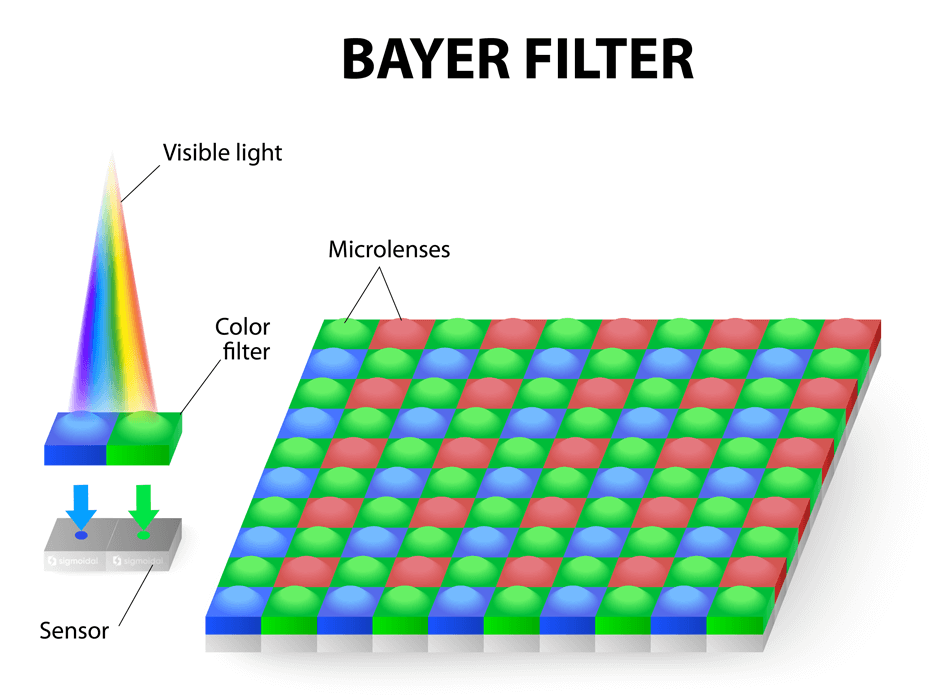
Entretanto, é relevante destacar que este é apenas um exemplo comum. Na prática, uma imagem digital pode ter mais bits e mais canais. Além do espaço de cores RGB, existem diversos outros espaços de cores, como o YUV, que também podem ser utilizados na representação e processamento de imagens digitais.

Por exemplo, durante o período que trabalhei no Centro de Operações Espaciais, recebia imagens monocromáticas com resolução radiométrica de 10 bits por pixel e hiperespectrais com centenas de canais para análise.

Resumo

Este artigo apresentou os fundamentos da formação de imagens, explorando os desafios da visão computacional, o processo óptico da captura, a relevância das lentes e a representação de imagens digitais.

No segundo artigo desta série, ensinarei como implementar um exemplo prático em Python para converter as coordenadas de um objeto real 3D para uma imagem 2D, e como realizar a calibração de câmera (uma das áreas mais importantes da Visão Computacional).

Referências

1. Szeliski, R. (2020). Computer Vision: Algorithms and Applications. Springer.
2. Gonzalez, R. C., & Woods, R. E. (2018). Digital Image Processing. Pearson Education.