Como usar OpenCV e Python para calibrar câmeras

Os olhos da equipe de cirurgiões estão fixos nas telas, onde cada movimento do robô cirúrgico é ampliado e analisado minuciosamente. O bisturi desliza suavemente pela pele do paciente, cortando camadas e camadas de tecido. O som é agudo e penetrante, ecoando pelo ar estéril da sala de cirurgia. Os médicos observam a cena atentamente, as mãos suando frio enquanto o robô cirúrgico executa seus movimentos precisos.

A sala de cirurgia é um lugar assustador, Iluminado apenas pela luz azul dos monitores que refletem a imagem da câmera, onde a vida e a morte caminham de mãos dadas. Afinal, mesmo com a equipe mais bem preparada, há sempre a possibilidade de falha. Os equipamentos utilizados na cirurgia podem apresentar problemas técnicos e os algortimos usados normalmente são desconhecidos.

Nesse ambiente de extrema pressão, um erro pode ser fatal. E é por isso que a calibração da câmera é tão importante.

Mas você já havia parado para pensar como a falta de calibração pode ser crítica em situações onde a precisão é fundamental, como em uma cirurgia robótica ou em uma operação militar? Imagine uma cirurgia robótica onde um milímetro de erro pode representar a morte do paciente. Ou imagine disparar um míssil a milhares de quilômetros de distância em um alvo militar, enquanto do lado há uma escola infantil. A distorção de lente e a calibração imperfeita de uma câmera podem levar a erros fatais em situações como essas.

Na área da pesquisa em visão computacional, técnicas de camera calibration têm elevado valor teórico e prático. Neste post, você aprenderá os conceitos básicos de calibração de câmera e como usá-los com o OpenCV e Python.

Fundamentos da calibração de câmera

A distorção de lentes é um fenômeno comum na captura de imagens e ocorre quando uma lente não consegue reproduzir com precisão a perspectiva de uma cena na imagem capturada.

Esse problema pode gerar distorções de forma e perspectiva na imagem, o que pode ser especialmente problemático em aplicações envolvendo visão computacional e realidade aumentada. Dentre as várias distorções existentes, as duas principais são a distorção radial e distorção tangencial.

A distorção radial ocorre quando os raios de luz que passam através da borda da lente são desviados em diferentes ângulos do que aqueles que passam pelo centro da lente. Isso pode resultar em linhas curvadas ou distorcidas nas bordas da imagem.

Já a distorção tangencial ocorre quando a lente não está perfeitamente alinhada com o sensor da câmera, o que pode resultar em linhas retas que parecem curvas ou inclinadas. É aquela sensação de que aquela moto do retrovisor parecia estar mais longe ou até mais próximos do que realmente estavam.

Felizmente, a distorção de lentes pode ser corrigida por meio da calibração da câmera, que envolve a medição da distorção de lentes e a correção dos dados da imagem de acordo com essas medições. Esse processo é especialmente importante em aplicações que exigem alta precisão, como a visão computacional em carros autônomos e sistemas de monitoramento de segurança.

Por que acontece a distorção?

É importante destacar que a distorção de lentes não é um problema exclusivo de câmeras de baixa qualidade ou baratas. Mesmo lentes de alta qualidade podem sofrer de distorção se não forem calibradas adequadamente.

Para entender, veja esse exemplo simples de uma modelo de câmera conhecido como pinhole (modelo de câmera pontual). Quando uma câmera foca em um objeto, ela o enxerga de maneira similar aos nossos olhos, concentrando a luz refletida no mundo real. Por meio de um pequeno orifício, a câmera concentra a luz refletida do objeto 3D em um plano na parte de trás da câmera.

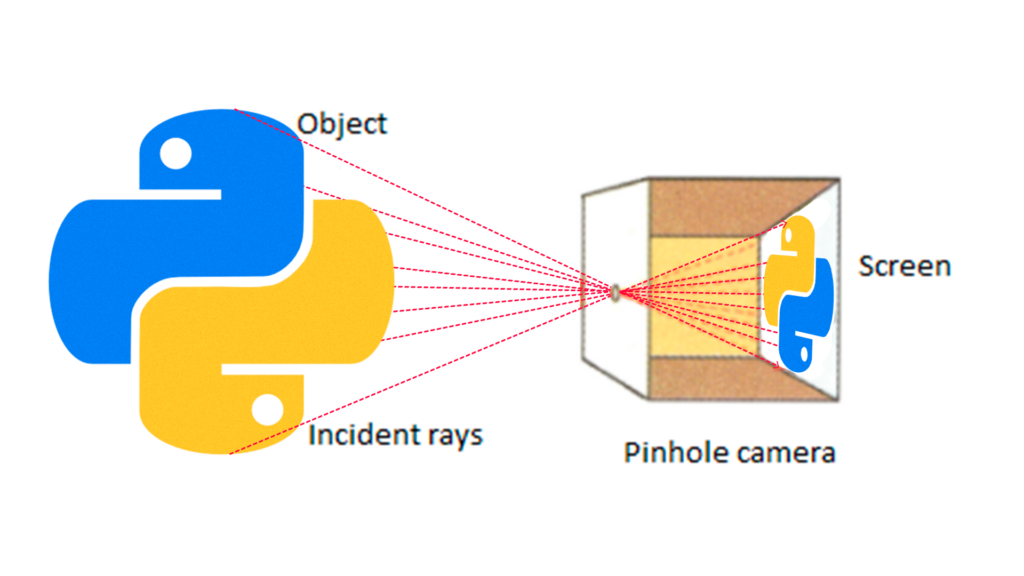
A matriz da câmera, que mapeia uma cena 3D em um plano de imagem 2D, é representada por uma matriz 3×4, também chamada de matriz de projeção. Essa matriz é composta pela multiplicação da matriz intrínseca pela matriz extrínseca. A matriz intrínseca, que representa os parâmetros internos da câmera, é dada por:

Onde e são as distâncias focais em pixels nas direções e , respectivamente. e são as coordenadas do ponto principal, ou centro óptico, da câmera na imagem em pixels. A última coluna da matriz é usada para calcular a projeção dos pontos 3D na imagem, mas não é necessária para a calibração da câmera.

A matriz extrínseca, que representa a posição e orientação da câmera no espaço 3D, é dada por:

onde u, v e w são as coordenadas homogêneas na imagem 2D. Para obter as coordenadas da imagem (x, y), basta dividir u e v por w:

Portanto, a calibração da câmera é uma etapa crucial em qualquer aplicação de visão computacional, que pode ter um impacto significativo na precisão e confiabilidade dos resultados obtidos.

Ao reconhecer a importância da calibração de câmera, os desenvolvedores podem garantir que suas soluções baseadas em visão computacional sejam confiáveis e eficazes, independentemente do ambiente ou das condições de captura de imagem.

Implementação da calibração de câmera com OpenCV e Python

Agora que compreendemos a importância da calibração de câmera e os fundamentos por trás disso, vamos abordar a implementação prática usando OpenCV e Python. O OpenCV é uma biblioteca de visão computacional amplamente utilizada e possui funções embutidas para realizar a calibração de câmera de maneira eficiente.

Preparação do ambiente

Primeiro, instale o OpenCV no seu ambiente Python, se você ainda não o fez. Você pode instalar o OpenCV usando o seguinte comando:

pip install opencv-python

Coleta de imagens

Antes de começarmos a implementar a calibração da câmera, é necessário coletar um conjunto de imagens de um padrão conhecido, como um tabuleiro de xadrez. As imagens devem ser tiradas em diferentes ângulos e posições para garantir uma calibração precisa. Neste exemplo, usaremos um conjunto de imagens de um tabuleiro de xadrez de 7×6.

Com o conjunto de imagens do tabuleiro de xadrez, podemos prosseguir para a detecção dos cantos do tabuleiro e a calibração da câmera. O código a seguir demonstra como fazer isso:

import cv2
import numpy as np
import glob

# Parâmetros do tabuleiro de xadrez
chessboard_size = (7, 6)  # Número de cantos internos no tabuleiro (largura x altura)

# Preparar pontos do objeto 3D
objp = np.zeros((np.prod(chessboard_size), 3), dtype=np.float32)
objp[:, :2] = np.indices(chessboard_size).T.reshape(-1, 2)

# Listas para armazenar pontos do objeto 3D e pontos da imagem 2D
object_points = []
image_points = []

list_of_image_files = glob.glob('./data/chessboard/*.jpg')

# Carregar e processar cada imagem
for image_file in list_of_image_files:
    image = cv2.imread(image_file)
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

    # Detectar cantos do tabuleiro de xadrez
    ret, corners = cv2.findChessboardCorners(gray, chessboard_size, None)

    # Se os cantos forem encontrados, adicione os pontos do objeto e da imagem
    if ret:
        object_points.append(objp)
        image_points.append(corners)

        # Desenhar e exibir os cantos
        cv2.drawChessboardCorners(image, chessboard_size, corners, ret)
        cv2.imshow('img', image)
        cv2.waitKey(500)

cv2.destroyAllWindows()

# Calibrar a câmera
ret, K, dist, rvecs, tvecs = cv2.calibrateCamera(
    object_points, image_points, gray.shape[::-1], None, None
)

print("Matriz de calibração K:\n", K)
print("Distorção:", dist.ravel())

Neste código, primeiro definimos o tamanho do tabuleiro de xadrez e preparamos os pontos do objeto 3D. Em seguida, carregamos as imagens do tabuleiro de xadrez e convertemos cada imagem para escala de cinza. Detectamos os cantos do tabuleiro de xadrez usando a função cv2.findChessboardCorners e armazenamos os pontos do objeto e da imagem correspondentes nas listas object_points e image_points.

Se os cantos forem encontrados com sucesso, desenhamos os cantos na imagem usando a função cv2.drawChessboardCorners e exibimos a imagem por um curto período de tempo.

Depois de processar todas as imagens, procedemos à calibração da câmera utilizando a função cv2.calibrateCamera, que recebe os pontos do objeto 3D, os pontos da imagem 2D e o tamanho da imagem em escala de cinza como argumentos. A função retorna a matriz de calibração K, os coeficientes de distorção, as matrizes de rotação e translação para cada imagem.

Ao final, imprimimos a matriz de calibração K e os coeficientes de distorção.

Agora que temos a matriz de calibração K e os coeficientes de distorção, podemos corrigir a distorção nas imagens usando a função cv2.undistort. Veja um exemplo de como fazer isso:

# Carregar uma imagem de teste
test_image = cv2.imread('./data/test_image.jpg')

# Corrigir a distorção da imagem
undistorted_image = cv2.undistort(test_image, K, dist, None, K)

# Exibir a imagem original e a imagem corrigida lado a lado
combined_image = np.hstack((test_image, undistorted_image))
cv2.imshow('Original vs Undistorted', combined_image)
cv2.waitKey(0)
cv2.destroyAllWindows()

Conclusão

A calibração da câmera é um aspecto crucial da visão computacional, especialmente em aplicações que exigem alta precisão, como cirurgia robótica e sistemas de monitoramento de segurança. Este artigo explorou os fundamentos da distorção de lente e a importância da calibração da câmera, além de apresentar uma implementação prática usando Python e a biblioteca OpenCV.

Ao entender os conceitos básicos e aplicar técnicas de calibração de câmera em suas soluções de visão computacional, os desenvolvedores podem garantir resultados mais confiáveis e eficazes, independentemente das condições de captura de imagem.

Além disso, a visão computacional é uma área em constante crescimento, oferecendo inúmeras oportunidades para aqueles que desejam aprimorar suas habilidades e conhecimentos nesta disciplina. Com a demanda por especialistas em visão computacional em ascensão, há uma abundância de vagas no exterior para profissionais qualificados. Aproveitar essas oportunidades pode abrir portas para uma carreira gratificante e diversificada, além de permitir que você contribua para o avanço da tecnologia e aprimore suas habilidades em um campo em rápido desenvolvimento.

Então, não hesite em mergulhar no mundo da visão computacional e explorar suas possibilidades, pois o futuro da tecnologia depende de mentes brilhantes e inovadoras como a sua.